퍼셉트론( perceptron )

퍼셉트론과 단층 퍼셉트론 ( single-layer perceptron )

퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 모델을 말한다.

• 입력으로는 입력 \(x\), 가중치 \(w\), 임계값 \(\theta\) 또는 편향 \(b(= -\theta)\)를 가진다.
• 뉴런에서 보내온 신호의 총합이 임계값을 넘어설 때 1을 출력한다.
• 입력 신호마다 각각의 가중치가 있는데, 가중치가 클 수록 해당 신호가 그만큼 중요함을 뜻한다.
• 임계값 \(\theta\)를 \(-b\)로 치환하여 사용한다. 편향 \(b\)는 뉴런이 얼마나 쉽게 활성화하느냐를 결정한다.

간단한 AND 회로를 퍼셉트론으로 옮기면 다음과 같은 형태다.

import numpy as np

  

def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w\*x) + b
if tmp <= 0:
return 0
else:
return 1

AND 회로의 동작을 만족하는 \(w_1, w_2, b\)값은 무수히 많다. 여기서는 \(0.5, 0.5, -0.7\)을 사용했다.

OR, NAND도 이런식으로 구현할 수 있지만 XOR은 단층 퍼셉트론으로는 구현할 수 없다. XOR은 선형 영역으로 나눌 수 없기 때문이다. 직선을 하나만 그어서는 1을 출력하는 영역과 0을 출력하는 영역으로 나눌 수 없다.

즉, 단층 퍼셉트론으로는 비선형 영역을 분리할 수 없다.

1. 곡선을 쓰거나, 2. Input Vector의 차원을 높이거나, 3. 직선을 여러 개 그어야 한다.
2. 곡선을 쓰게 되면 느리고, 만들기 어렵고, overfitting 문제도 있다.
3. 이렇게 차원을 올려 해결하는 방식이 SVM이다.
4. 직선을 더 긋는(뉴런을 추가해 층을 더 쌓는) 방식으로 해결하는 모델이 NN이다.

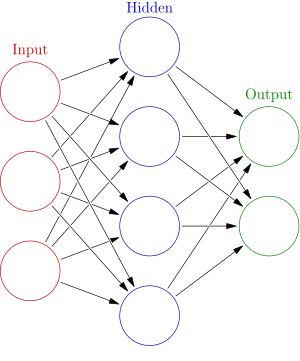
다층 퍼셉트론 ( multi-layer perceptron )

XOR은 NAND, OR, AND를 하나씩 사용해 구현할 수 있다. NAND, OR를 통과시킨 결과를 AND에 통과시키면 XOR이 되는데, 이렇게 이전 출력을 다음 입력으로 사용하게 되는(가중치가 적용 되는) 단계를 층이라고 부르고 층이 여러 개인 퍼셉트론을 다층 퍼셉트론이라 한다.

제일 왼쪽 층을 입력층, 중간을 은닉층, 맨 오른쪽 층을 출력층이라 한다. 은닉층의 뉴런은 가시적으로 확인이 불가능하기 때문에 은닉층이라 부른다. n층 신경망일 경우, 입력층은 0층, 1 ~ n-1층은 은닉층, n층은 출력층이다. (층의 개수는 n+1층이지만 실제로 가중치를 갖는 의미있는 층은 n층이므로 n층 신경망이라 한다.)

NAND, OR, AND의 조합으로 XOR을 만들어 낸 것 처럼, 퍼셉트론으로 기존 컴퓨터가 수행하던 처리를 모두 표현할 수 있다. 층을 증가시켜 가며 AND 게이트에서 반가산기 전가산기로, 그 다음은 ALU, 그 다음은 CPU를 만들어 낼 수 있는 것이다.

아무튼 중요한 것은 층을 쌓아 비선형적 표현도 가능하며 복잡한 함수도 표현할 수 있다 는 것이다.

참고

밑바닥부터 시작하는 딥러닝 http://aikorea.org/cs231n/