인공신경망 ( ANN ) 6-3 최적화 - 오버피팅 방지( weight decay, droupout ) / 하이퍼파라미터 최적화
오버피팅( Overfitting )
오버피팅은 훈련 데이터에만 지나치게 적응하여 시험 데이터에 제대로 반응하지 못하는 현상을 말한다. 주로 다음 경우에 발생한다.
- 매개변수가 많고 표현력이 높은 모델인 경우
- 훈련 데이터가 적은 경우
Regularization
오버피팅을 억제하기 위해서 다음과 같은 regularization 기법을 사용한다. regularization은 일반화 정도로 번역될 것 같다. 신경망이 범용성을 갖도록 처리하는 거니까. normalization, 정규화와는 다르다.
weight decay ( L2 regularization )
L2 regularization은 가장 일반적으로 사용되는 regularization 기법으로, 오버피팅은 가중치 매개변수의 값이 커서 발생하는 경우가 많기 때문에 가중치가 클 수록 큰 페널티를 부과하여 오버피팅을 억제하는 방법이다. 여기서 페널티 부과란 가중치 리스트가 W 일 때 손실 함수의 결과에 \(\frac{1}{2} \lambda WW^{T}\)을 더하는 것을 말한다. * λ는 정규화의 강도를 조절하는 하이퍼파라미터. 크게 설정할 수록 가중치에 큰 페널티가 부과된다. * 각 layer의 가중치에 해당하는 각각의 가중치 벡터
손실 함수에

이에 따라서 가중치 W 갱신이
손실 함수의 결과에
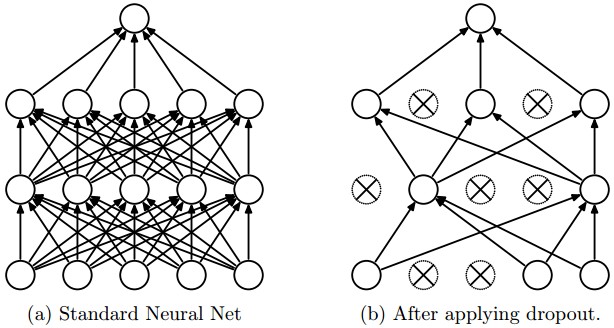
Dropout
다른 regularization 기법들과(L1, L2, maxnorm) 상호 보완적인 방법으로 알려져 있다. 드롭아웃은 각 계층 마다 일정 비율의 뉴런을 임의로 정해 drop시켜 나머지 뉴런들만 학습하도록 하는 방법이다. 이는 네트워크 내부에서 이루어지는 ensemble learning이라고 생각해도 좋다. * ensemble learning(앙상블 학습)은 개별적으로 학습시킨 여러 모델의 출력을 종합해 추론하는 방식이다. dropout과 별개로 실행 시점에 따로 적용할 수 있다. 뉴럴 네트워크를 개별적으로 학습시키고, 각 네트워크에 같은 input을 주어 나온 출력 뉴런 각각의 평균을 구한 다음 여기서 가장 큰 값을 정답으로 판정하면 되기 때문에 간단히 구현할 수 있다. e.g. ) ( network1.output[1] + network2.output[1] ) / 2 = ensemble_output[1]
역전파는 ReLU처럼 동작한다. 순전파 때 신호를 통과시킨 뉴런은 역전파 때도 그대로 통과시키고, drop된 뉴런은 역전파 때도 신호를 차단한다.
test 때는 모든 뉴런에 신호를 전달해아 한다는 것에 주의한다. 단, test 때 각 뉴런의 출력에 훈련 때 삭제한 비율을 곱해서 출력한다고 하는데, 곱하지 않아도 잘 돌아가는 것 같다.
하이퍼파라미터 최적화
하이퍼파라미터의 성능을 평가할 때 시험 데이터를 사용하면, 하이퍼파라미터의 값이 시험 데이터에 오버피팅 되기 때문에 시험 데이터를 사용하지 않고 따로 검증 데이터(validation data) 를 만들어 평가한다. 검증 데이터를 따로 두어도 좋고, 훈련 데이터의 일부를 검증 데이터로 사용할 수도 있다. 중요한 것은 시험 데이터는 말그대로 범용성 평가용으로 사용해야하지, 최적화 용으로 사용해서는 안된다는 것이다.
하이퍼파라미터 최적화는 대략적인 범위를 설정하고 그 범위에서 무작위로 값을 선택해 정확도를 평가한 다음 좋은 정확도를 내는 곳으로 범위를 축소하는 방식을 반복한다.
어느정도 범위가 좁아지면 그 범위 내에서 값을 하나 골라낸다. * gird search 같은 규칙적 탐색 보다는 무작위로 샘플링해 탐색하는 것이 좋은 결과를 낸다고 한다.
범위는 보통 10의 거듭제곱 단위로 지정 한다. 이를 로그 스케일(log scale)로 지정한다고 한다.
딥러닝 학습에는 시간이 오래 걸리기 때문에 학습을 위한 에폭을 작게 하여 1회 평가에 걸리는 시간을 단축하는 것이 효과적이다.
이런 방법 말고, 수학적 이론을 기반으로 한 하이퍼파라미터 최적화 방법으로는 Bayesian optimization 이 있다.
practical-bayesian-optimization-of-machine-learning-algorithms.pdf
데이터 확장 (data augmentation)
훈련 이미지의 개수가 적을 때, 이미지를 회전하거나 이동, pixel shift하는 등 미세한 변화를 주어 훈련 데이터의 수를 늘리는 방법. 간단하지만 효과가 꽤나 좋아서 훈련 데이터가 부족할 때 사용하면 좋다.
전이 학습 (transfer learning)
미리 학습된 가중치를 초깃값으로 설정한 다음 새로운 데이터를 대상으로 재학습하는 것.
참고
밑바닥부터 시작하는 딥러닝
http://aikorea.org/cs231n/neural-networks-2-kr/
https://jamesmccaffrey.wordpress.com/2017/02/19/l2-regularization-and-back-propagation/
http://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf
- dropout