선형 시간 안에 중앙값 선택하기
최악의 경우에도 선형 시간에 중간값 을 선택할 수 있는 알고리즘은 다음과 같다.
아래는 median을 찾는 예이지만, k번째 작은 값 찾는 문제에 적용 가능하다.
Element select(SetOfElements S, int k)
- 중앙값만 찾는 거라면 k 파라미터가 필요 없지만, 일반적인 선택 문제로 확장하면 k 파라미터가 필요함.
- k는 몇번째로 큰 값을 찾을건지. k번째로 작은 값을 찾는다.
k=n/2를 넘기면 중간값을 찾겠다는 것.
알고리즘 (k번째 작은 값 찾기를 이용해 median 찾는 예제)
1. 입력 배열이 n개라면 원소 5개짜리 \(\lceil n/5 \rceil\) 그룹으로 나눈다.
- 마지막 집합은 \(n \mod 5\)개 원소를 가질 수 있다.
2. 각 그룹에서 중앙값(_m)을 찾는다. 중앙값을 찾는 데는 다음 방법을 사용한다.
3. 이제 중앙값들의 중앙값(median of median, m)을 찾아야 하는데, 어차피 이도 중앙값을 찾는 문제이므로 select()를 한 번 재귀호출한다. m = select(M, M/2);
M은_m들로 이루어진 집합(배열)을 의미한다.M/2를 넘기므로 개수가 짝수일 경우 내림 되어m은 더 앞에 있는 중앙값이 된다.
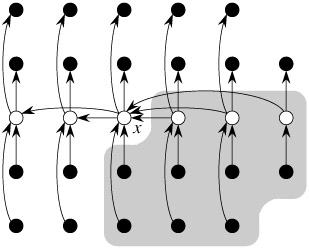
4. (x=m) x를 기준으로 x보다 큰 원소는 S1 그룹, x보다 작은 원소는 S2 그룹으로 분할한다.
- x를 기준으로 [우측 & 하단](회색영역)에 있는 모든 원소는 x보다 크다. ->
S2 - x를 기준으로 [좌측 & 상단]에 있는 모든 원소는 x보다 작다. ->
S1 - 나머지 영역 [우상단&좌하단]에 대해서는 대소를 알 수 없으므로 x와 직접 비교해 알맞은 그룹으로 넣는다.
5. 분할 정복으로 해결한다.
* 중간값 찾는 경우 k = n/2 가 된다.
1
2
3
4
5
6
if (k == sizeof(S1) + 1)
return m;
else if (k <= sizeof(S1)) // k번째 작은 값을 찾을건데 S1에 원소 개수가 k보다 크다면? k번째 작은 값은 S1에 있다.
return select(S1, k);
else
return select(S2, k - (sizeof(S1) + 1));
수행 시간 분석
계산이 간단하도록 n이 5의 홀수 배라고 가정한다. 1-2. 5개의 키 집합들에 대한 중앙값을 구하는 데는 5개의 원소의 중앙값을 찾는데 6번 비교하는 알고리즘을 사용했다고 가정하면 \(6*(n/5)\)번 비교.
- 중앙값들의 중앙값을 찾는데 재귀를 사용하기 때문에 \(W(n/5)\)번 비교.
x를 기준으로 확실히 x보다 작은 원소의 개수는 \[(\frac{n}{5} - 1) \frac{1}{2} 3 + 2 = \frac{3n}{10} + \frac{1}{2} \] x보다 확실히 큰 원소의 개수도 n이 5의 홀수배이면 위와 같다. 따라서 대소를 알 수 없는 영역에 속하는 원소의 개수는 \( \approx 4n/10 \) 이므로, 이 만큼 비교.
- 분할 정복법으로
select()를 재귀 호출 하는데, 최악의 경우는 예를들면 찾으려는 k가S1에 속해있는데 대소를 알 수 없는 영역을 비교해보았더니 모든 원소가 x 보다 작아S1에 들어가는 경우이다. \( S1.size = 3n/10 + 4n/10 \) 이 되므로 \(W(7n/10)\) 만큼 비교.
\[W(n) \le \frac{6n}{5} + W(\frac{n}{5}) + \frac{4n}{10} + W(\frac{7n}{10})\] 점화식을 푸는데 재귀 트리를 이용해도 좋고(Computer Algorithms, Sara Baase) 수학적 귀납법을 이용해도 된다.(Introduction to algorithms)
재귀트리를 이용해 구해보면 \(16n\)이 나오는데, 최악의 경우 \(2.95n\)번 비교하는 알고리즘도 존재하기는 하나 꽤 복잡하다. in-place는 아니지만 재귀의 깊이가 \(O(\lg{n})\)이므로 공간적인 부분이 많이 필요하지는 않다.
하한선
현재 최선의 하한선은 \(2n\) 정도로 알려져 있다.